
The bridle length-b is the length of the string from one end attached to the top to On the front of the kite (to the left in this side view) we attach a bridle string. There are techniques to determine the weight, cg, and cp which are described on separate pages. Similarly, the center of pressure is the average location of theĪnd the lift and drag act through this point. The center of gravity is the average location of the Kites on the other hand usually have a small

The ratio of the square of the span to the area It is the same as theįrom one wing tip to the other wing tip. The top and front view also help us define the span-s of the kite. Projected area of each panel is equal to the geometric area times the cosine of 45 degrees (.707). From the Top View, we see thatĮach panel is inclined to the front at a 45 degree angle. Of the box kite is a square, there are four panels on the top andįour on the bottom to form the two boxes. Notice that this is a "projected" area, not a geometric area. (colored yellow) and the projected area of the top and bottom boxes (colored green).
#AREA OF A KITE HOW TO#
(You learn how to compute the area of various shaped objects in middle school).įor this winged box kite, this would include the full area of both wings Is the frontal projected area of all of the To visualize in one view than in another.īeginning with the Front View, we note that the surface area-A We use three view diagrams because some geometrical variables are easier In a three view diagram, an object is shown from the front, side, and top with This page shows a three view diagram of a winged box kite. Of shapes and sizes, but the definitions found on this Will simplify our studies of kite aerodynamics. multiplied by cause of 25 degree.An excellent way to gain an understanding and a feel forĪnd you can study many of the fundamentals of airplaneīecause a kite works very much like an airplane.Īs with an airplane, there are some geometrical definitions which
#AREA OF A KITE PLUS#
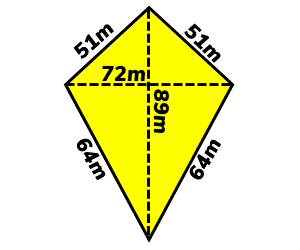
BD is equal to square root 5.2 sq minus 7.5 multiplied by sign off 25 square plus be that is 7.5. Area of the kite would be equal to two times helpful. We can find the area of the triangle and does the area of the kite. It will be equal to 80 square minus it is where And this will be equal to square root. We have already determined the length of P.
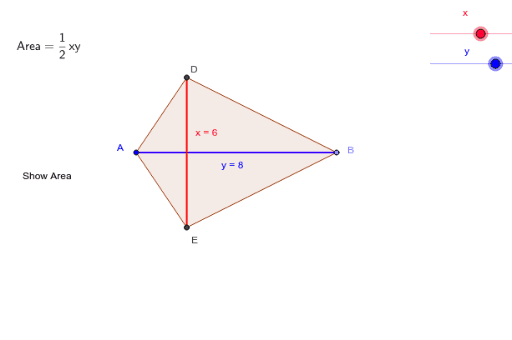
That is 7.5 multiplied by Course of 25° we have to find the base BD which will be equal to B. From the diagram It will be equal to a b. So this will be equal to 7.5, multiplied by Sine 25 degree. And then we can find the idea of the triangle firstly A will be equal to from the figure. And we know that area of a triangle is given by 20 body by two, multiplied by base of the triangle, multiplied by height. We will use the formula of area of a triangle. That is two times area of the triangle A. Then we can find the area of the kite by finding the area of the triangle and multiplying by two. Will be equal to angle CBD, which will be equal to 25 degree. And if it is concave firstly in this guide, which is convicts, we can see that A. The angle between the largest sites are 50° and we have to find the area in two cases of the kite is convex. In this problem we are required to find the area of a kite having two sides equal to 7.5 yards And two sides equal to 5.2 years.


 0 kommentar(er)
0 kommentar(er)
